今天是主題 DAG，另外看一下昨日文章 討論二元樹直徑的擴展題。

DAG (directed acyclic graph):

• 是有向圖且沒有環的圖稱為 DAG

DAG 可以用來表示依賴關係
如下，可以代表 完成 2 之前需要完成 1。

[1] -> [2]  

節點 [1] 指向 節點 [2]，節點1的 out-degree = 1, in-degree = 0
節點 [2] 被指向，節點2的 in-degree = 1，out-degree = 0

DAG 的應用場景除了如以下 leetcode 題外，也用於作業系統裡檢查是否發生 deadlock等情況，檢查是否陷入僵局。額外參考資料: Deadlock-free Mutexes and Directed Acyclic Graphs

拓譜排序

用拓譜排序檢查圖是否為 DAG!

拓譜排序簡單就是

1. 把所有in-degree = 0 的節點當作已經排序好的節點，從圖上in-degree 為0的節點移掉，之後要更新這些節點指向的節點的 out-degree
2. 重複這過程，直到這張張圖不存在有 in-degree 為0 的節點

拓譜排序過程:
gif 的來源: FJCU CPC 訓練網 -- 有向無環圖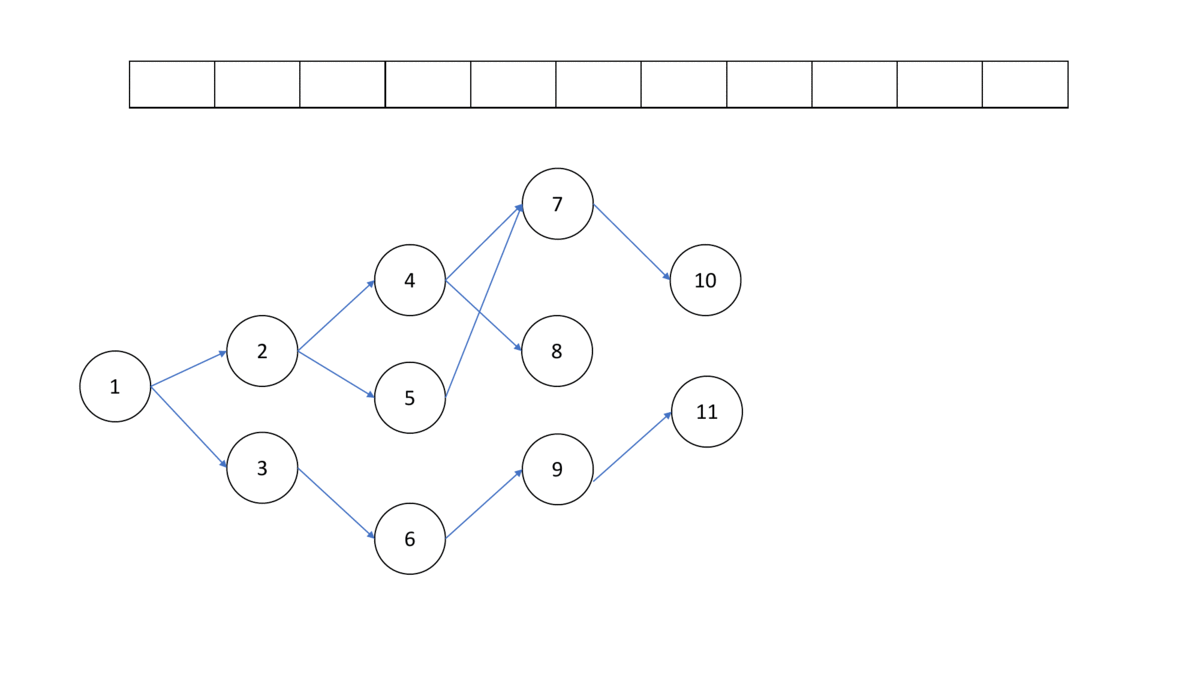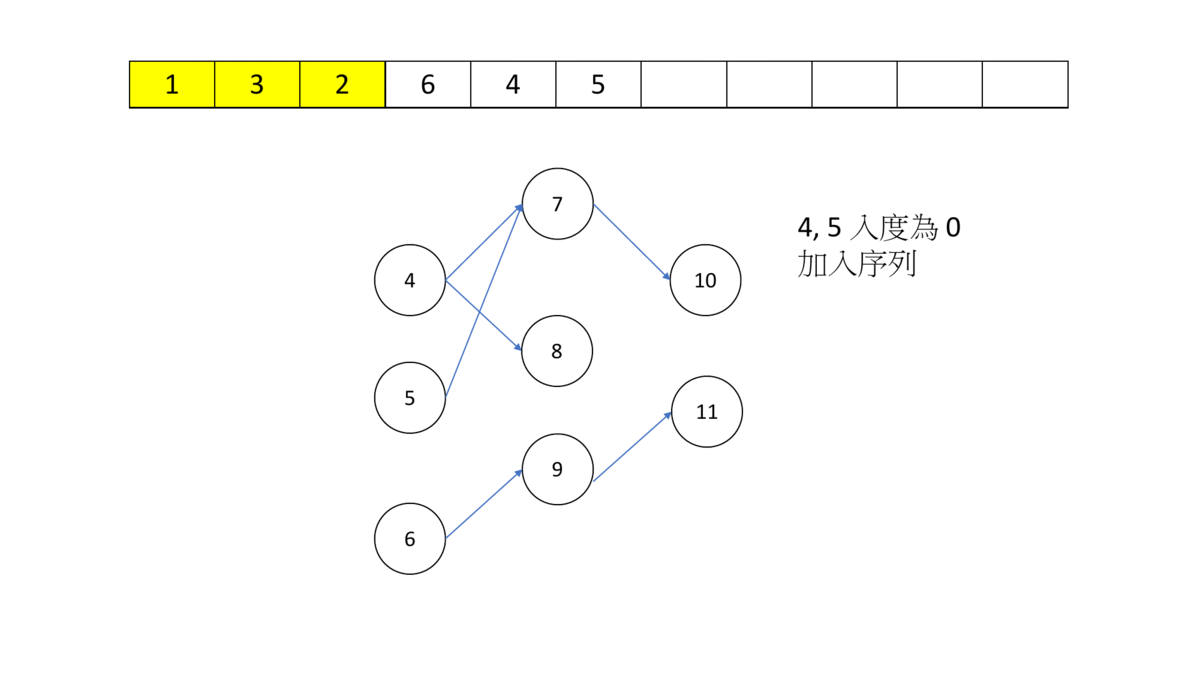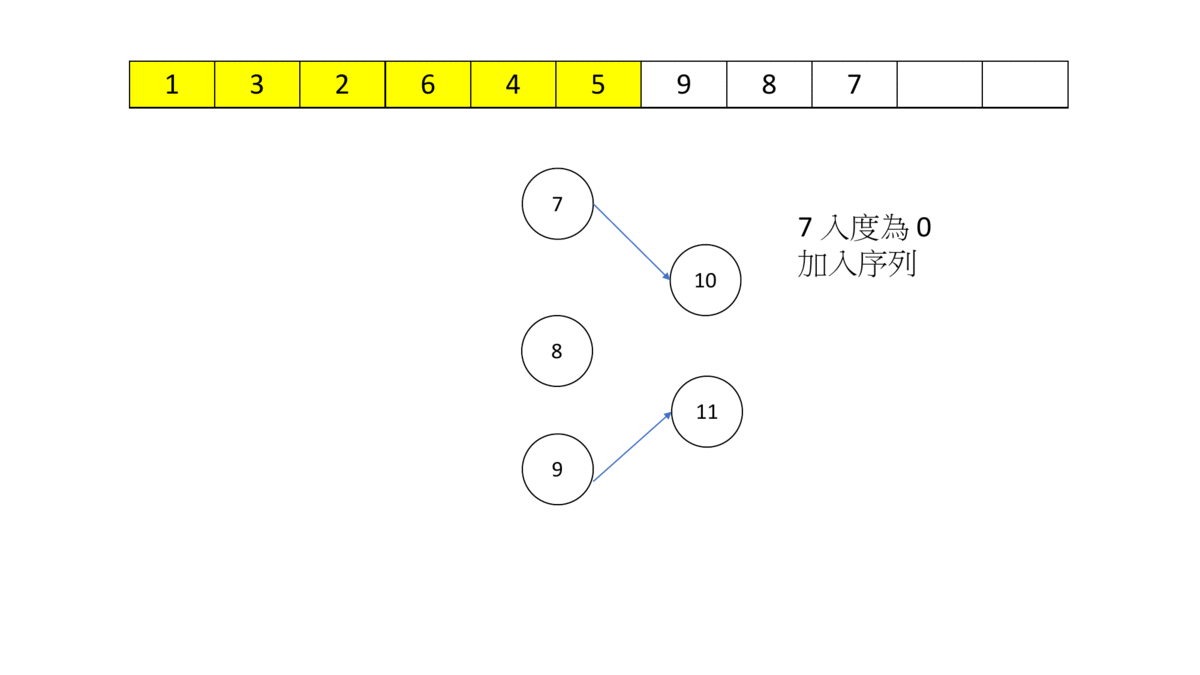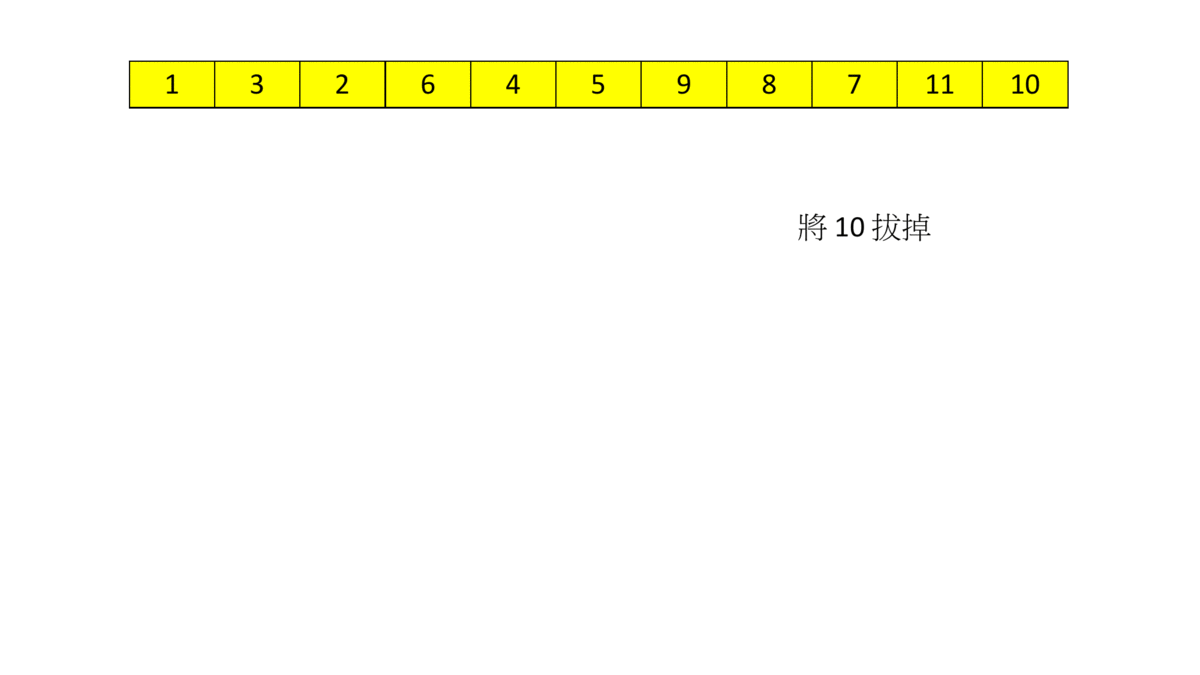

倘若排序完畢後仍有節點的 in-degree 大於 0，那麼說明圖中存在環。

舉個反例:

[0] -> [1] --> [2]
	    ^       |
		| ------|

拓撲排序會排好節點 0，但在節點 1 和節點 2 的 in-degree 無法降為 0，最終無法完成排序，說明圖中存在環。

207. Course Schedule (medium)

題目敘述
幫助學生完成課程排序。題目給一個整數 numCourses 代表需要修的課程總數，還有一個表示先修條件的二維陣列 prerequisites。在 prerequisites 中，每一對 [a, b] 表示課程 a 需要先完成課程 b。

因此可以視為

[b] → [a]

輸入範例

Input: numCourses = 2, prerequisites = [[1,0],[0,1]]

[0] → [1]
↑      ↓
←------

這兩門課互為先修條件，出現循環，因此無法修完所有課程。

解題思路

使用拓撲排序來判斷是否出現迴圈? 答案為否，那就代表存在某選課順序能修完課程。

1. 建立入度與鄰接表
   • 用 deg[i] 表示課程 i 的in-degree，也就是課程 i 需要的先修課數量。
   • 用 adj[i] 表示課程 i 是哪些課程的先修課（out-degree）。
2. 拓撲排序的過程
   • 首先，將所有入度為 0 的課程加入 taken 表示這些課程可以開始學習。
   • 然後，不斷將這些課程移出圖般，並將其影響的課程的in-degree 減少 1。
3. 判斷
   如果能完成所有課程（即 taken 的數量等於 numCourses），則表示可以修完所有課程；否則圖中有環，無法完成。

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<int> deg(numCourses, 0);
        vector<vector<int>> adj(numCourses);
	    // Create in-degree array (deg) and adjacency list (adj)
        for(auto edge: prerequisites) {
            deg[edge[1]] += 1;
            adj[edge[0]].push_back(edge[1]);
        }
        vector<int> taken;
        for (int i = 0; i < numCourses; i++) {
            if (deg[i] == 0) taken.push_back(i); //First add all courses without prerequisite courses
        }
        int idx = 0; // Use the index to track which courses have been processed
        while(idx < taken.size()) {
            int in_0 = taken[idx++]; // Get a course that can be taken
            for (int n: adj[in_0]) {
	            // If the in-degree of the course is 0, it can be taken
                if (deg[n] > 0 && --deg[n] == 0) { 
                    taken.push_back(n);
                }
            }
        }
        if (idx != numCourses) return false;
        return true;
    }
};

時間複雜度: O(V + E)，其中 V 是課程數量（節點），E 是先修課的數量（邊）。需要遍歷所有的節點和邊來完成拓撲排序。

1522.Diameter of N-Ary Tree

這是 昨天講到的543. diameter of binary tree (easy) 的擴展題，但題目在 leetcode 上需要是會員才能看到。
我在 github 上有人分享其解題: 1522.Diameter of N-Ary Tree
題目從 binary tree 上找直徑改成 N-ary Tree上找。

但解題概念與昨日我的解法相似。

int dfs(Node* root)
遞迴回傳的值仍是樹高，此解題的差異在於，要嘗試 root 的所有小孩節點並知道他們的最大高度時，另外還需要更新小孩間兩個最大高度(m1, m2, m1> m2)。如果 root 是直徑的中間節點，那麼直徑會是 m1 + m2，因為這代表了經過 root 的兩條最長路徑，因此更新全域變數 ans ，這變數是用來追蹤所有節點中的最大直徑。